G検定の学習として、今回はコアの機械学習を勉強していきます。
G検定の概要はこちらに書いていますので、G検定に興味があれば、こちらも御覧ください。(2020年6月26日(金)まで、7月のG検定受験料半額キャンペーン中です。)
機械学習の種類概要(教師あり・教師なし・強化学習)
それぞれ向き不向きがあり、どういった課題を解決するのかで変わってきますので把握しておくことが大事です。
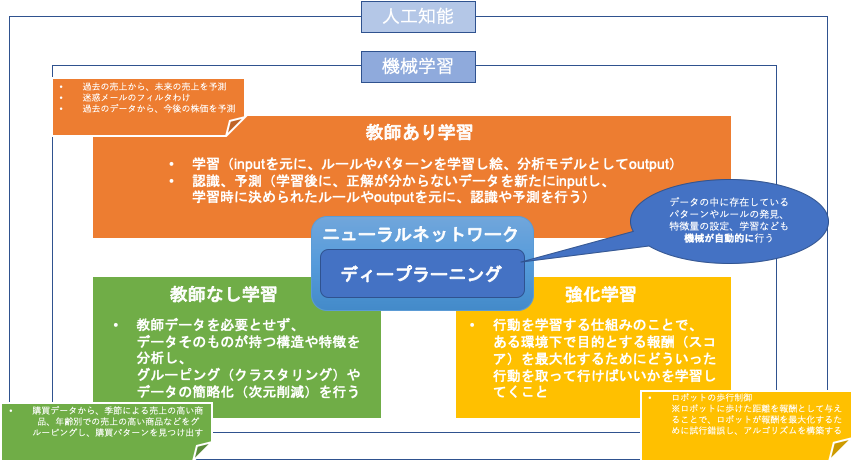
教師あり学習
与えられたデータ(input)を元に、そのデータがどんなパターン(output)になるのかを識別・予測するものです。

例えば、
- 過去の売上(input)から、将来の売上を予測(output)
- メールのフィルタリング
- 翻訳
回帰問題
連続値を予測する問題は、回帰問題といいます。
例えば、売上を予測する場合は、過去がありこれからの数値を出したい = 連続値を予測 となるので、回帰を使います。
別の言い方をすると、outputが実数の値であるものをいい、連続出力内で結果を予測し入力変数をいくつかの連続関数にマッピングするということをします。
分類問題
離散値を予測する問題は、分類問題といいます。
例えば、与えられた動物の画像がなんの動物なのかを識別する場合には、連続値ではないので、分類を使います。
別の言い方をすると、outputがカテゴリであるものをいいます。結果を離散出力で予測します。
教師なし学習
大きな特徴は、教師なし学習で使うデータには、outputが無いことです。
※教師 = output(出力データ)のこと
inputデータそのものが持つ特徴や構造を対象とし、関係性を見つけたりする場合に使います。
クラスタリングなどが有名です。

例えば、
- ECサイトの売上データから、顧客層の特徴を把握する
- 入力したデータの項目間にある関係性を把握する

教師あり学習と教師なし学習は、データセットの形式に違いがあります。
教師あり学習は、入力データと出力データが、
教師なし学習は、入力データのみが用いられます。
さらに
教師あり学習は、データ間の関連性を学習し、
教師なし学習は、データが持つ構造や特徴を学習します。
強化学習
行動を学習する仕組みを強化学習といいます。
一連の行動をとった結果ごとに報酬を設定し、その報酬が最大化するように機械が試行錯誤して学習することで精度を上げていくものです。

例えば、
- ロボットの歩行制御
※ロボットに歩けた距離を報酬として与えることで、ロボットが報酬を最大化するために試行錯誤し、アルゴリズムを構築する
一見すごく良さそうなこの強化学習ですが、状態をいかに表現できるか、その状態に基づいていかに現実的な時間内で行動に結びつけることができるのかがとても難しいです。
教師あり学習の手法
線形回帰(Linear Regression)
データの分布があったときにそのデータに最も当てはまる直線を考えるというもの。
最もシンプルなモデルの1つ。
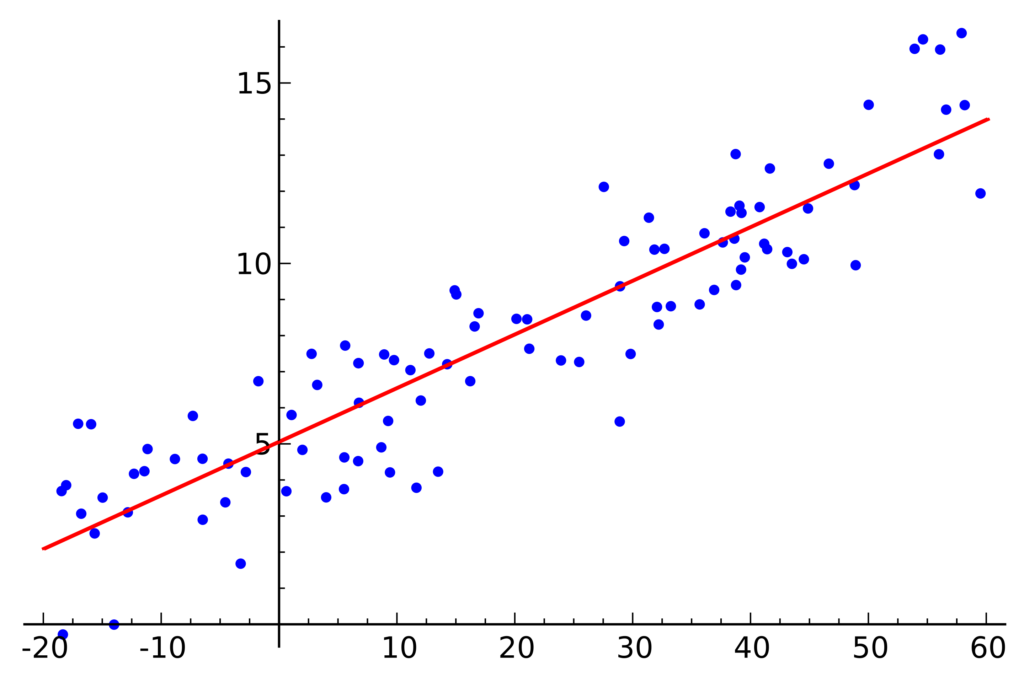
2次元でなくても、もっと次元が大きくても対応可能で、
線形回帰に正則化(データ全体を調整する処理)項を加えたラッソ回帰(Lasso Regression)や、リッジ回帰(Ridge Regression)もあります。
→ 参考:最短でリッジ回帰とラッソ回帰を説明(機械学習の学習 #3)
ロジスティック回帰
名前に回帰が入っていますが、回帰問題ではなく分類問題に用いる、でおなじみなニューラルネットワークがこのロジスティック回帰(Logistic Regression)です。
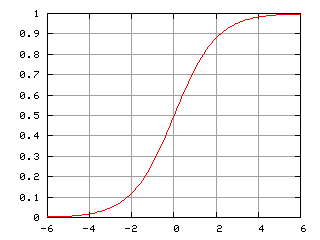
これは、シグモイド関数をモデルの出力に使います。
任意の値を、0〜1の間に写像することで与えられたデータが正例(+1)になるのか、負例(0)になるのかの確率が定まり、
出力値が0.5以上なら正例、0.5未満なら負例と設定しておけば、データを2種類に分類できるというわけです。
→ 基本は、0.5を閾値にして正例と負例を分類するのですが、0.7や0.3などにすることで、分類の調整を行うこともできる。
→→ 調整の例としては、迷惑メールの識別の場合通常のメールが迷惑メールに判定されると良くないので、予め閾値を高めに設定しておくなどがあります。
さらに、
もっとたくさんの種類の分類を行いたいという場合には、シグモイド関数の代わりに、ソフトマックス関数を使うことになります。
ランダムフォレスト
ランダムフォレスト(Random Forest)は、決定木(Decision Tree)を使う方法です。
特徴量がどんな値になっているかを順々に考えて分岐路を作っていくことで、最終的に1つのパターンである output を予測できるという、
この分岐路が決定木になります。
ただ、「どんな分岐路を作るのがいいのか?」についてはデータが複雑になるほど組み合わせがどんどん増えてくるので、
ランダムフォレストでは特徴量をランダムに選び出し、複数の決定木を作るという手法を取ります。
データも全部を使うのではなく、一部のデータを取り出して学習に使うようになります(ブートストラップサンプリング)

ランダムに選んだデータに対して、ランダムに決定木を複数作成して学習するから、
ランダムフォレスト!
で、
複数の決定木を作成するので、予測結果は決定木で異なる場合が発生しますが、ランダムフォレストではそれぞれの結果を以って、多数決を取ることによりモデルの最終的な出力を決めています。
ランダムフォレストのように、複数のモデルで学習させることを、アンサンブル学習といいます。
全体から一部のデータを用いて複数のモデルを用いて学習する方法をバギングといいます。

バギングの中で、決定木を用いている手法が、
ランダムフォレストになります。
ブースティング(Boosting)
ブースティングは、バギングと同様に一部のデータを繰り返し抽出し、複数のモデルを学習させる方法です。
バギングとの違いとしては、以下になります。
- バギング・・・複数のモデルを並列で作成する方法
- ブースティング・・・複数のモデルを逐次的に作成する方法
ブースティングの場合は、1つのモデルを作成し学習させ、次に作成するモデルではそこでご認識してしまったデータを優先的に正しく分類できるように学習させていきます。
つまり、順次1つ前のモデルで誤認識してしまったデータに重みをつけて学習を進め、最後には1つのモデルとして出力させるのです。
逐次的に学習を進めていくぶん、精度はランダムフォレストよりも高いですが、並列処理ができない分、時間がかかるという側面もあります。

ブースティングも、モデルで決定木が使われています。
サポートベクターマシン(Support Vector Machine, SVM)
サポートベクターマシンは、inputの各データ点との距離が最大となるような境界線を求めることで、分類(パターン分析)を行うものです。
基本は、2分類問題を解くために使われ、
多クラス分類を解く際には、決定木やニューラルネットワークを用います。
この距離を最大化することを、マージン最大化といい、誤データをどれだけ許すのかはエンジニアが事前に調整しておくことが求められます。(ハイパーパラメータ)
しかし、以下の問題があります。
データが高次元になることに関しては、超平面(二次元の平面をそれ以外の次元へ一般化)することで解消できますが、
線形分類できない問題に関しては、なにをもってマージンが最大化となるのかを考える必要があります。
そこで、
SVMでは、あえてデータを高次元に写像させることでその写像後の空間で線形分類できるようにするというアプローチになります。
写像に使われる関数を、カーネル関数といい、その際に計算が複雑にならないように式変形するテクニックをカーネルトリックといいます。
ニューラルネットワーク(Neural Network)
ニューラルネットワークは、人間の脳の中の構造を模したアルゴリズムです。
人間の脳にある、ニューロンの特徴を再現しようとしているアルゴリズムで、
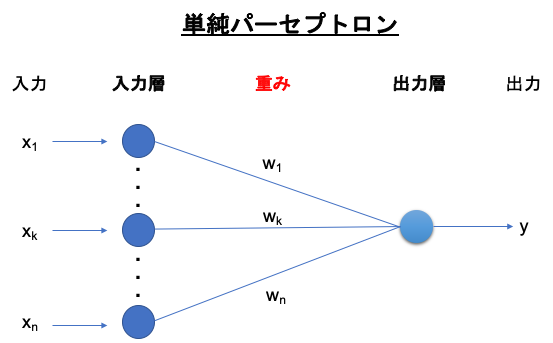
1958年にフランク・D・ゼンブラッドの単純パーセプトロン(Simple Perceptron)が単純なニューラルネットワークのモデルの1つです。

単純パーセプトロンは、複数の特徴量(入力)を受け取り、1つの出力を行います。

パーセプトロンを使って溶ける問題は、
「直線を使って分離できるもの」= 線形分離可能
なものです。
ニューラルネットワークは層構造
人間の脳は神経回路が層構造になっているため、ニューラルネットワークでも入力を受け付ける入力層と出力をする出力層があります。
入力層の各ニューロンと出力層の各ニューロン間の繋がりは、重みとして表され、どれだけの電気信号を伝えるかを調整しています。
※出力が0か1の値を取るようにすることで、正例と負例を分類できることになります。
出力を0〜1の値を取るように閾値の調整を行うことも可能です。その場合は、シグモイド関数を使って表現します。(ロジスティック回帰)
このシグモイド関数のように、層の間をどのように電気信号を伝播させるかを調整する関数のことを総じて、活性化関数と言ったりします。

ただ、この単純パーセプトロンでは線形分類しかできない単純すぎるアルゴリズムだったため、
更に層を追加していこう!
というアプローチになっていきました。
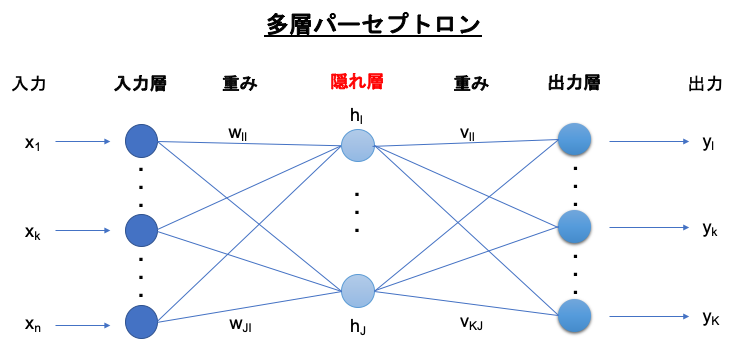
これを多層パーセプトロン(Multi-layer Perceptron)といいます。
多層パーセプトロンには、隠れ層が存在する
多層パーセプトロンでは、入力層と出力層の間に隠れ層が存在し、非線形分類を行うことも可能になりました。
層が増えるということは調整するべき重みも増えてくるということになりますので、
予測値と実際の値との誤差をネットワークにフィードバックするアルゴリズムの誤差逆伝播法(Backpropagetion)が考えられました。
教師なし学習
教師なし学習は、入力データにある構造や特徴を掴むためのものです。
k-means法
k-means法は、データをk個のグループ(クラスタ)に分けることを目的としたアルゴリズムです。
→ 元のデータから、グループ構造を見つけ出し、それをまとめるということ。

このkは自分で設定する必要がある値です。

グループのことを、クラスタ(Cluster)といい、k-means法を使った分析を、クラスタ分析といいます。
k-means法のアプローチをまとめると、以下のようになります。
- 適当に各データをk個のクラスタに分ける
- 各クラスタの重心を求める
- 求まったk個の重心と各データとの距離を求め、各データを最も距離が近い重心に対応するクラスタに振り分け直す
- 重心の位置がほぼ変化しなくなるまで、2と3を繰り返す
主成分分析(Principal Component Analysis, PCA)
主成分分析は、データの特徴量間の関係性、相関を分析することでデータの構造をつかむ手法です。
特に、
特徴量の数が多いときに使われ、相関を持つ多数の特徴量から、相関のない少数の特徴量へと次元削減することが主目的になります。
ここで得られる少数の特徴量のことを主成分といいます。
機械学習の手法評価
機械学習の目的は、手元のデータを学習することでデータの特徴を掴み、未知のデータが与えられたときにそれがどういったパターンになるのかを識別・予測できるようになることです。
どれがどのくらいの予測性能を持っているのかを評価する必要があり、どのように評価すればいいのかを知る必要があります。
上記から、モデルの評価も未知のデータに対しての予測能力を見ることが適切です。

え?
でも、評価する未知のデータを準備できないよ。。。

そういう場合には、手元のデータから、擬似的に未知のデータを作り出すということをします。
擬似的に未知のデータを作り出す
手元の全データを、学習用のデータ(訓練データ)と評価用のデータ(テストデータ)にランダムに分割して評価します。
このようにデータを分割して評価することを、交差検証といいます。
ただ、ここでまた問題が、、、
全体のデータ数が少ない場合、たまたまテストデータに対する評価が良くなるという可能性が出てきます。
これを防ぐため、訓練データとテストデータの分割を複数回行って、それぞれで学習と評価を行うというアプローチ(k-分割交差検証)をとることもあります。
※ちなみに基本的に訓練データとテストデータを事前に分割しておくことをホールドアウト検証といいます。
訓練データをさらに分割する場合もありその場合はそれぞれ、訓練データと検証データと呼びます。
評価指標

例えば、10,000枚の犬と狼の画像を使って、別の2,000枚の画像が犬か狼家を予測する問題を考えてみます。
これは、訓練データが10,000枚、テストデータが2,000枚ということになりますので、
混合行列(Confusion Matrix)にしてみます。

混合行列の中で、予測があたっているのは
真陽性と真陰性になるので、そこから正解率を求めることができます。
正解率(Accuracy) =
真陽性のデータ数(TP)+ 真陰性のデータ数(TN)/ 全データ数(TP+TN+FP+FN)
正解率を出すのが適している場合もありますが、100,000個の部品から数個あるかどうかの不良品を識別する場合には正解率から求めると、99.99x%みたいな使えない数値を求めることになってしまうので、
何を評価したいのかを明確にしておく必要があります。
指標のまとめ
正解率(Accuracy)
全データ中、どれだけ予測があたったのかの割合です。
Accuracy = TP + TN / TP + TN + FP + FN
適合率(Precision)
予測が正の中で、実際に正であったものの割合です。
Precision = TP / TP + FP
再現率(Recall)
実際に正であるもののなかで、せいだと予測できた割合です。
Recall = TP / TP + FN
F値(F measure)
適合率と再現率の調和平均です。
適合率のみ、あるいは再現率のみで判断すると予測が偏っているときも値が高くなってしまうのでF値を用いることも多いです。
F measure = 2 × Precision × Recall / Precision + Recall

いずれの指標を使うにせよ、
モデルの性能はテストデータ(及び検証データ)
を用いて評価・比較するということに注意しましょう。
オーバーフィッティング(Overfitting)
オーバーフィッティングは、機械学習において最も注意すべき問題の1つで、
訓練データに対してモデルを合わせ込みすぎることで新しいデータに対する汎用性能が失われてしまうことです。(過学習)
例えば、正則化(過学習を抑制するための方法)は、
学習の際に用いる式に項を追加することによってとりうる重みの値の範囲を制限し、過度に 重みが訓練データに対してのみ 調整されることを 防ぐ役割を果たします。

アンダーフィッティング(Underfitting)
アンダーフィッティングは正則化など、過学習を調整しすぎると全体の汎化性能(予測性能)が低下してしまうことを言います。
やりすぎはだめってことですね。
正則化
よく使われる正則化項としては、以下があります。
- L1正則化・・・
一部のパラメータの値をゼロにすることで、特徴選択を行うことができる
この手法をラッソ回帰といいます。 - L2正則化・・・
パラメータの大きさに応じてゼロに近づけることで、汎化されたなめらかなモデルを得ることができる。
この手法をリッジ回帰といいます。
この2つを組み合わせた手法を、Elastic Netといいます。
参考資料
深層学習教科書 ディープラーニング G検定(ジェネラリスト) 公式テキスト (日本語) 単行本(ソフトカバー)
徹底攻略 ディープラーニングG検定 ジェネラリスト 問題集 徹底攻略シリーズ Kindle版